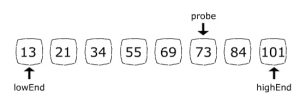
المعطى مصفوف مرتبة من العناصر والمطلوب ايجاد عنصرمعين وليكون x فى المصفوفة []arr
باستخدام Interpolation Search خوارزمية وهى نسخة محسنة من خوارزمية البحث الثنائى binary search حيث ان خوارزمية البحث الثنائى تذهب دائمًا للعنصر الاوسط فى المصفوفة لتقارن العنصر المراد ايجاده به اما فى حالة Interpolation search فان موقع العنصر فى المصفوف سيختلف باختلاف قيمة العنصر الذى نبحث بمعنى انه اذا كان العنصر المراد البحث عن اقرب إلى العنصر الاخير فإن Interpolation search ستبدء بالبحث فى نهاية المصفوفة (وليس فى الوسط مثل binary searc ) اما اذا كان العنصر المراد البحث عنه اقرب إلى العنصر الاول فان الخوارزمية ستبدء البحث فى البداية ولإيجاد موقع العنصر المناسب عن طريق المعادلة التالية
// pos فكرة عمله المعادلة هى ارجاع قيمة كبيرة ل // arr[hi]عندما يكون العنصر الذى نبحث عنه اقرب إلى العنصر الاخير // arr[lo] وارجاع قيمة صغيرة اذا كان العنص اقرب للعنصر الاول pos = lo + [ (x-arr[lo])*(hi-lo) / (arr[hi]-arr[Lo]) ]
arr[] ==> المصفوفة التى سنبحث فيها
x ==> العنصر الذى سنبحث عنه
lo ==> مكان اول عنصر فى المصفوفة
hi ==> مكان اخر عنصر فى المصفوفة
خطوات عمل الخوارزمية
الخطوة الاولى : فى داخل اللوب نقوم نحسب pos عن طريق المعادلة السابقة
الخطوة الثانية : اذا كان العنصر الذى نبحث عنه مطابق للعنصر فى المصفوفة الذى مكانه pos ترجع الخوارزمية True
الخطوة الثالة : اذا كان العنصر الذى نبحث عنه اصغر من العنصر الذى مكانه pos فنحسب pos مره اخرى للجزء الشمال من المصفوفة اما اذا كان العنصر اكبر فنتعامل على الجزء اليمين من المصفوفة
التكرار حتى الوصول إلى العنصر المطلوب
الكود التقريبى باستخدام cpp
// If x is present in arr[0..n-1], then returns
// index of it, else returns -1.
int interpolationSearch(int arr[], int n, int x)
{
// Find indexes of two corners
int lo = 0, hi = (n - 1);
// Since array is sorted, an element present
// in array must be in range defined by corner
while (lo <= hi && x >= arr[lo] && x <= arr[hi])
{
// Probing the position with keeping
// uniform distribution in mind.
int pos = lo + (((double)(hi-lo) /
(arr[hi]-arr[lo]))*(x - arr[lo]));
// Condition of target found
if (arr[pos] == x)
return pos;
// If x is larger, x is in upper part
if (arr[pos] < x)
lo = pos + 1;
// If x is smaller, x is in lower part
else
hi = pos - 1;
}
return -1;
}
استدعاء الدالة
// Driver Code
int main()
{
// Array of items on which search will
// be conducted.
int arr[] = {10, 12, 13, 16, 18, 19, 20, 21, 22, 23,
24, 33, 35, 42, 47};
int n = sizeof(arr)/sizeof(arr[0]);
int x = 11; // Element to be searched
int index = interpolationSearch(arr, n, x);
// If element was found
if (index != -1)
printf("Element found at index %d", index);
else
printf("Element not found.");
return 0;
}
الخرج
Element found at index 4
زمن التنفيذ هو ((o(loglog(n وفى اسوء حالة worst case هى (o(n

