-:Definition
The minimum of operations required to convert one string into other such as:-
•Deletion
•Insertion
•replace
Operations:-
•Deletion •Insertion •substitute
•Gold •Gold •Gold
• Old •Goaled •sold
•Edit distance = 1 2 1
Edit Distance:-
•Edit distance depends on the available operations.
•The edit distance that allows……
(Insertion,deletion,replace)
•Operations is the levenshtien distance
Levenshtien distance:-
•Devised in 1965by Vladimir levenshtien a Russian scientist .
•Some terminology:-
A string S S1 , S2 , S3 ,………….,Sn caterpillar n = 11
A substring S1…k S1 …….. Sk,………….,Sn caterpillar k = 3
To find the edit distance between string S and T It’s handy to examine their sub strings……
Sn and Tm
S1….j T1….k
for all jfrom n-1 to 1 for all kfrom n-1 to 1
Edit distance:-
•E[ j , k ] = D(S1….j ,T1….k)
•E[ j , 0 ] = D(S1….j , “ ” ) = j deletion
•E[ 0 , k ] = D( “ ” ,T1….k) = k insertion
Computation of the edit distance:-
•E[ j , 0 ] = j
•Distance of any string of length jto empty string
•E[ 0 , k ] = k
•Distance from empty string to string of length k
deletion E[ j-1 , k ] + 1
insertion E[ j , k-1 ] + 1
do no thing E[ j-1 , k-1 ] Sj=Tk
substitute E[ j-1 , k-1 ] +1 Sj=Tk
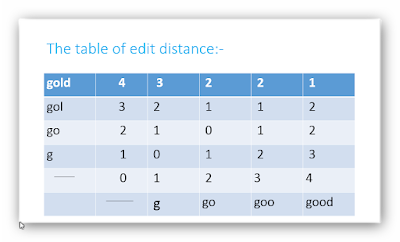
The table of edit distance:-
An algorithm for edit distance:-
time complexity:-
The time complexity of above solution is exponential.
Time Complexity: O(m x n)
Auxiliary Space: O(m x n)
Applications:-
Edit distance finds applications in computational biology and natural language processing, e.g. the correction of spelling mistakes or OCR errors, and approximate string matching, where the objective is to find matches for short strings in many longer texts, in situations where a small number of differences is to be expected
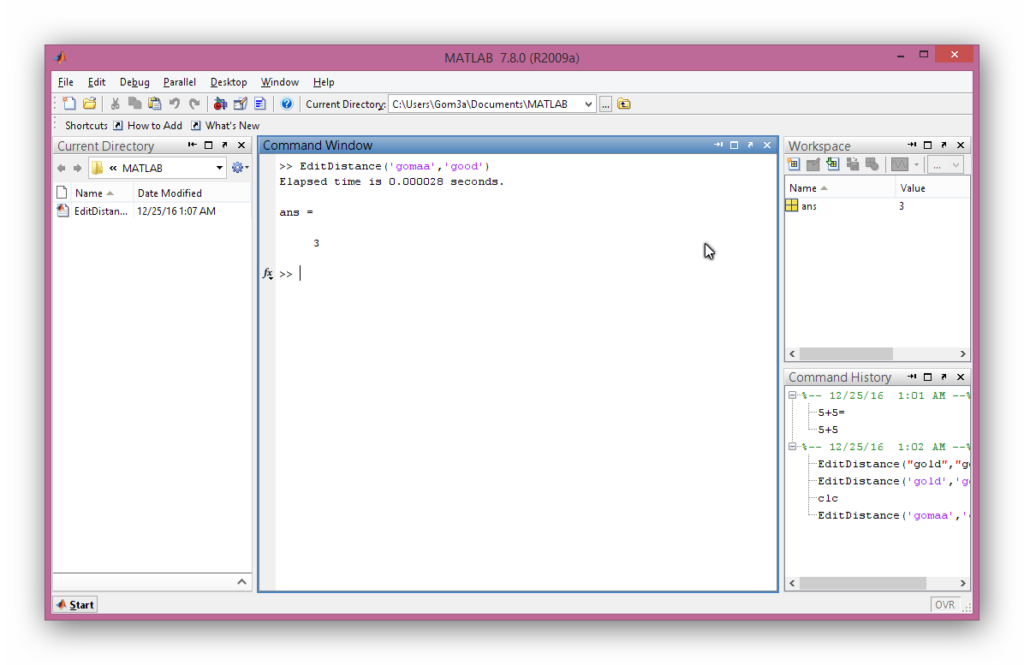
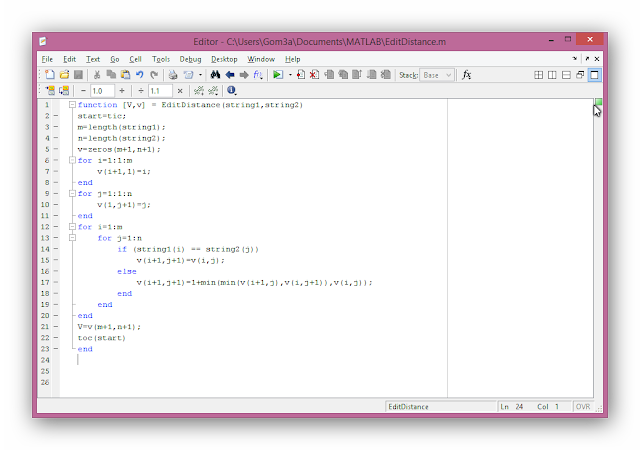
Matlab Code:-
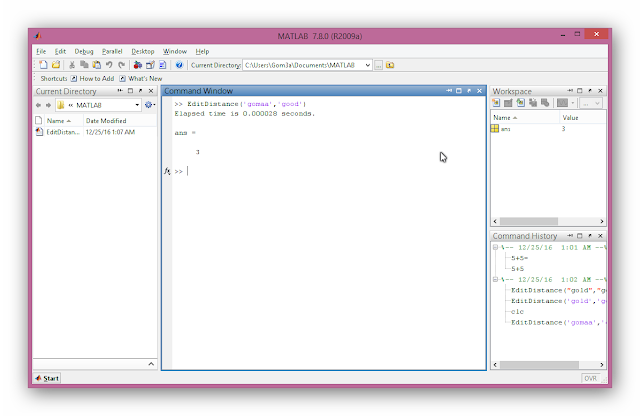
Result of Run:-
Thank you