محتوي المقال
كيف تعمل خوارزمية البحث الثنائي
كغيرها من الخوارزميات لا بد من توافر المدخلات المطلوبة و التي تتمثل في العُنصر المراد البحث عنه و المصفوفة التي سيتم البحث فيها
يجب أن تكون المصفوفة مرتباً تصاعدياً (من الأصغر إلى الأكبر)، في حال لم تكن المصفوفة مرتبة تصاعدياً يجب عليك أن تُرتبها تصاعدياً حتى تستطيع تطبيق خوارزمية البحث الثنائي
مصفوفة البحث لها فهرس (Index) يبدأ من الصفر أو الواحد، لكليهما نفس النتيجة
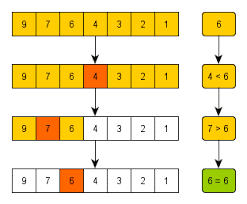
تبدأ الخوارزمية عملها بوضع مؤشر الفهرس في وسط المصفوفة حتى تقسم المصفوفة إلى قسمين، و هنا بداية الإستفادة الفعلية من مبدأ (فرّق تسُد)
إذا خطر على بالك هذا التساؤل “توجد مصفوفات عدد عناصرها زوجي و أخرى عدد عناصرها فردي فكيف يكون مؤشر المصفوفة في الحالتين في الوسط” فأهنئُك على هذا التفكير. إن عملية إختيار وسط المصفوفة بسيطة و سهلة، كل ما عليك إتباع المعادلة التالية
 و تعني هذه المعادلة (floor( (low + high) /2 فيكون وسط مصفوفة عناصرها 5 هو العنصر الثاني، و وسط مصفوفة عناصرها 4 أيضاً العنصر الثاني.
و تعني هذه المعادلة (floor( (low + high) /2 فيكون وسط مصفوفة عناصرها 5 هو العنصر الثاني، و وسط مصفوفة عناصرها 4 أيضاً العنصر الثاني.


- تتم مقارنة العنصر بالوسط (حيثُ المؤشر) بالعُنصر المُراد البحث عنه و النتيجة إحدى ثلاث حالات:
أن تساوي قيمة العُنصر بالمصفوفة قيمة العُنصر المُراد البحث عنه، و بالتالي يتم الإحتفاظ بقيمة مؤشر الفهرس و يُوقف البحث.


أن تكون قيمة العُنصر المراد البحث عنه أكبر من قيمة العنصر حيث المؤشر، في هذه الحالة يتم تجاهل جميع عناصر النصف الأيسر من المصفوفة و يُصبح الجزء الأيمن من المصفوفة مُدخلاً جديداً لعملية بحث عن طريق خوارزمية البحث الثنائي.


أن تكون قيمة العُنصر المراد البحث عنه أقل من قيمة العنصر حيثُ المؤشر، في هذه الحالة يتم تجاهل جميع عناصر النصف الأيمن من المصفوفة و يُصبح الجزء الأيسر من المصفوفة مُدخلاً جديداً لعملية بحث عن طريق خوارزمية البحث الثنائي.


تُكرر عملية البحث (الخطوة 6) في النصف المتُبقي حتى يتم الوصول إلى خانة واحدة فقط تُمثل موقع العنصر المُراد البحث عنه.
مهمة الدالة floor هي إيجاد أكبر قيمة صحيحة ( ليست كسر) أقل من القيمة المُستقبلة في الدالة. أمثلة : floor(3.9) = 3 ، floor(100.1) = 100 ، floor(-10.3) = -11
حساب أفضل و أسواء حالة لخوارزمية البحث الثنائي
أفضل حالة بالنسبة لخوارزمية البحث الثنائي: أعتقد أنها بينة كالشمس، فعندما يكون العُنصر المراد البحث عنه في وسط المصفوفة، فسيوجد في أول لحظة للبحث، بالتالي تكون هذه أفضل حالة لحالات خوارزمية البحث الثنائي.
أسوأ حالة لخوارزمية البحث الثنائي : أحتاج منك إلى تركيز، كُن معي. عُد إلى الصورتين السابقتين بالأعلى التين نتجاهل بهما الجزئين الأيمن و الأيسر في مصفوفة البحث الثنائي لمصفوفة ذات عدد عناصر زوجي.
إحسب عدد عناصر المصفوفة المتبقية عندما تجاهلنا الشق الأيمن من المصفوفة و عندما تجاهلنا الشق الأيسر. أرجو أن تكون لاحظت الإختلاف، و إن لم تلاحظ سأوضحه لك الآن.
إحسب عدد عناصر المصفوفة المتبقية عندما تجاهلنا الشق الأيمن من المصفوفة و عندما تجاهلنا الشق الأيسر. أرجو أن تكون لاحظت الإختلاف، و إن لم تلاحظ سأوضحه لك الآن.
عندما تكون المصفوفة ذات عدد عناصر فردي (لنفرض 9)، و نختار العُنصر الأوسط حيث نضع مؤشر الفهرس (العنصر رقم 5) تتبقى 4 عناصر من اليمين و كذلك 4 عناصر من اليسار، ما يعني أن العُنصر إذا كان أكبر أو أصغر من العُنصر الأوسط فإن عدد العناصر التي تم تجاهلها سيكون 5 ( 4 عناصر بأحد الإتجاهين بالإضافة إلى العُنصر الوسطي).
تظهر المُشكلة عندما يكون عدد عناصر المصفوفة زوجي، فإذا كان عدد عناصر المصفوفة 8، فوفقاً لمعادلة إختيار وسط المصفوفة المذكورة أعلاه يكون وسط المصفوفة هو العنصر رقم 4، بالتلي تتبقى 4 عناصر من الإتجاه الأيمن و 3 في الإتجاه الأيسر، أليس كذلك؟!!
تظهر المُشكلة عندما يكون عدد عناصر المصفوفة زوجي، فإذا كان عدد عناصر المصفوفة 8، فوفقاً لمعادلة إختيار وسط المصفوفة المذكورة أعلاه يكون وسط المصفوفة هو العنصر رقم 4، بالتلي تتبقى 4 عناصر من الإتجاه الأيمن و 3 في الإتجاه الأيسر، أليس كذلك؟!!
و هنا يأتي إستنتاج مهم و هو ما تُبنى عليه أسوأ حالة في حالات خوارزمية البحث الثنائي، و هو بما أن :
عدد عناصر المصفوفة إما فردي أو زوجي
عندما يكون عدد عناصر المصفوفة فردي فإن عدد العناصر المتبقية يتساوى
عندما يكون عدد عناصر المصفوفة زوجي فإن عدد العناصر المتبقية في الجانب الأيمن أكبر من الأيسر
فإن أسوأ حالة لخوارزمية البحث الثُنائي هي عندما يكون العُنصر المُراد البحث عنه أكبر من جميع العناصر بالمصفوفة.
صورة توضح الفرق بين الية عمل binary serch و linear search وكيف ان binary search اسرع بكثير
Binary Search Pseudo Code الكود التقريبي لخوارزمية البحث الثنائي
بلغة البايثون
def binarySearch(alist, item):
first = 0<br> last = len(alist)-1
itr=0
while first<=last:
midpoint = (first + last)//2
print('nclosest items = ',alist[midpoint])
if alist[midpoint] == item:
return True
else:
if item < alist[midpoint]:
last = midpoint-1
else:
first = midpoint+1
return False
testlist = [0, 1, 2, 8, 13, 17, 19, 32, 42]
print(binarySearch(testlist, 4),'n')
print(binarySearch(testlist, 13),'n')


